One of the key parts of The Forest is the gradual exploration of the dense woods that make up the game board. Typically your character will start in a clearing and then youā€™ll be able to navigate along roads and paths to the next adjacent hex. The first step (after generating the background) is to choose where the player starts, work out where the player needs to get to, and then create a random path from point A to point B. This is called ā€œpath generationā€ and is something Iā€™ve been focused on for the last week or so.

To begin with, I have a scenario JSON file which will dictate the fixed elements of the current scenario. It looks something like this presently:

{
    "title": "In the beginning",
    "map": {
        "columns": 8,
        "rows": 8,
        "start": {
            "environment": "clearing",
            "distanceFromBoardEdge": 0
        },
        "finish": {
            "minimumDistanceFromStart": 6,
            "maximumDistanceFromStart": 9
        }
    }
}

Weā€™re most interested in the map section which defines the basic size of the map (8 by 8) and gives us a rough indication of where to start and finish; in this case, weā€™re going to place a ā€œclearingā€ tile somewhere on the edge of the grid and have the finish be 6 to 9 hexes away from the start. This sense of randomness should mean that scenarioā€™s can be replayed and still feel fresh; there will be story beats that are consistent but the random layout and random encounters should keep it interesting.

In my first iteration of the path finding code, I thought the easiest solution would be to pick my random starting hex, pick the distance (if there is a min/max), and then generate every single possible route before picking one at random. Doing this is relatively straightforward:

func possibleRoutesToVictory(from start: String) -> Set<String> {
    let distance = Int.random(in: finish.minimumDistanceFromStart...finish.maximumDistanceFromStart) + 1
    var routes = Set<String>()
    enlargeRoute(start, routeDistance: distance, routes: &routes)
    return routes
}

private func enlargeRoute(_ route: String, routeDistance: Int, routes: inout Set<String>) {
    let references = route.components(separatedBy: "-")
    guard references.count < routeDistance else {
        routes.insert(route)
    }
    
    guard let reference = references.last else {
        fatalError("Could not get last reference")
    }
    
    guard let maxColumn = columns.toAlphabet(), let gridReference = reference.toGridReference() else {
        fatalError("Could not create maxColumn or gridReference")
    }
    
    let neighbours = gridReference.neighbours(maxColumn: maxColumn, maxRow: rows).filter({!references.contains($0)})
    for neighbour in neighbours {
        enlargeRoute("\(route)-\(neighbour)", routeDistance: routeDistance, routes: &routes)
    }
}

Our possibleRoutesToVictory function is given the starting hex position, picks the length of the route, and then creates an empty Set that can hold strings. The strings in this set will look something like A1-B2-B3-C3-C2-C1-D1 and denote the grid reference of the hexes the route proceeds through; this set is returned at the end of the method so we can then pick a route to render.

The main part of the process is calling a recursive function named enlargeRoute that takes a route string, distance, and our routes set. It separates the passed route into grid references and checks to see if the count is equal to the hex distance weā€™re looking for. If it is, the string is put into the routes set as a valid path and the method exited. If not, we check all of the neighbours1 of the last hex in the route and run this method again on every hex that isnā€™t already present in the route thus potentially spawning up to 6 new routes. In this way, we gradually increase the length of the route and create new routes until weā€™ve gone through every single possible iteration.

Once completed, we have a set of route strings and we can pick one at random to use as our route. For a journey with a distance of 6 hexes this translates into just over 4000 choices for us to choose from:

A few of the ~4000 six-hex routes that are generated in around 0.1 seconds
A few of the ~4000 six-hex routes that are generated in around 0.1 seconds.

This seems great in theory but it quickly unravelled when I tried longer paths. For example, a distance of 10 hexes turned into 788,550 possible routes taking 7 seconds to generate. Thatā€™s not going to work. šŸ˜‚

My first thought is that things are obviously quicker when weā€™re working in smaller chunks as there are far less choices. I thought I could maybe break the routes into pieces by turning a 12 hex route into three sets of 4 hex routes. That could potentially lead to a lot of dead ends though as it would be easy for the hexes to get trapped against a wall or corner which would then mean the routes could never complete (and whilst I could mitigate that by regenerating the initial 4 hex seeds and starting again it was getting a bit convoluted).

Instead, the final version was painfully simple. In the code above Iā€™m generating every single route but what if I just stopped inserting into the set after 1 route is generated? With the current code that would mean the path would always be the same as the neighbours are tested in the same order every time but randomising that would lead to the result I was looking for.

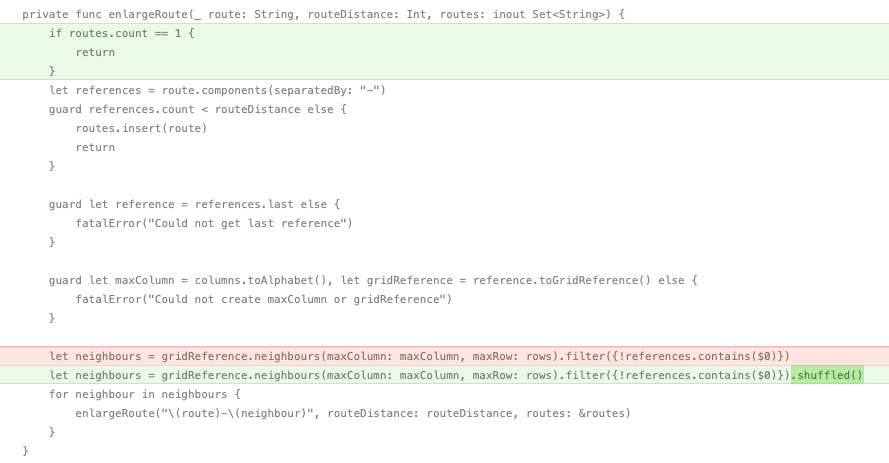
A diff showing the simple fix for generating a single path
A diff showing the simple fix for generating a single path.

All I needed to do was shuffle the array of hex neighbours that are returned and then exit the function once a single route is found. This leads to paths being generated in a mere 2 milliseconds, even when they are 40 hexes long.

A random forty-hex route generated in 2 milliseconds
A random forty-hex route generated in 2 milliseconds.

The end result works well as it runs until it finds a valid route; if the random nature of the first route ends in a spiral that means we canā€™t get to the full length of the route then it doesnā€™t matter as it will keep iterating through every choice until a single route is found, then stop to avoid wasting further cycles on a solved problem.

With this now working as intended, the next step is to start drawing a path on top of the hex tiles before beginning the process of adding some dead ends and shortcuts throughout the map.

  1. The calculation for the neighbours of a hex is fairly simple translating the current grid reference and then determining what the 6 hexes around it will be. It needs a maxColumn and maxRow as we donā€™t want to return hexes that are on the outside of the bounds of the board. We already know not go below 0,0 so we donā€™t require a minimum.Ā ↩︎